Макроструктури въ пъзлитѣ отъ рода на пентомината и хексиамантитѣ

Въ търсене какво да се реди съ пъзлитѣ на рода на пентомината и хексиамантитѣ, първата идея, която хрумнала, била за прости форми съ симетрична форма, като най-симетричнитѣ форми сѫ най-престижни. Така напримѣръ, отъ пентомината се редятъ правоѫгълници, защото квадратитѣ сѫ невъзможни съ 60 квадратчета. Възможенъ е квадратътъ 8 × 8 съ дупка 2 × 2 точно въ центъра, но формитѣ съ дупка сѫ второразрядни. При хексиамантитѣ е невъзможна фигура съ шесть оси на симетрия, но пъкъ голѣма популярность има форма, която може да бѫде завъртѣна шесть пѫти на по 60° (вж. фиг. 1, въ лѣво). Едностраннитѣ хексиаманти, за които сѫществува форма съ шесть оси на симетрия, сѫ изслѣдвани дори по-рано отъ самите хексиамантитѣ, най-вѣроятно именно поради наличието на тази форма (вж. фиг 1, въ срѣдата). При хептиамантитѣ такава форма сѫщо сѫществува и сѫщо е популярна (фиг. 1, въ дѣсно). 

Фиг. 1. Формата въ срѣдата нѣма дупка, дебело очертаниятъ шестоѫгълникъ е участваща въ пъзела фигурка.

Слѣдъ като се провѣри осѫществимостьта на разнообразнитѣ симетрични форми, правятъ се опити въ областьта на макроструктуритѣ, за които искамъ да говоря: редятъ се форми, които сѫ съставени отъ голѣми блокове, които сѫ на свой редъ по възможность симетрични. Така напримѣръ, при фигуркитѣ съставени отъ квадрати се пробватъ форми, съставени отъ по-голѣми квадрати. Желателно е да се използватъ всички фигурки отъ набора, но това не винаги е възможно. Пентомината могатъ да образуватъ максимумъ петь голѣми квадрата съ страна три и обща площь 45 квадратчета. Тази задача се нарица трипликация или, казано по-просто, утрояване (фиг. 2).

Фиг. 2. Примѣръ за утрояване на пентомино, взетъ отъ сайта https://www.cimt.org.uk/resources/puzzles/pentoes/penttrip.htm.

Нѣщата ставатъ особено интересни при фигуркитѣ съставени отъ триѫгълници и шестоѫгълници. Да вземемъ за примѣръ хексиамантитѣ. Тѣхната обща площь е 72 триѫгълничета, но 72 = 6 × 12 = 24 × 3, слѣдователно трѣбва да се пробватъ форми, съставени отъ дванадесеть шестоѫгълника съ страна едно или отъ три шестоѫгълника съ страна двѣ. Оказва се, че и двѣтѣ възможности сѫ осѫществими, както се вижда по-долу.

Фиг. 3. Горната форма е съставена отъ дванадесеть шестоѫгълника съ страна едно, а долната отъ три със страна двѣ. 

Формитѣ, образувани отъ тритѣ голѣми шестоѫгълника, обаче, сѫ чисто и просто тритѣ трихекса. Така се появява една връзка между фигурки отъ триѫгълници и отъ шестоѫгълници, въ което нѣма нищо изненадващо, защото един шестоѫгълникъ може да бѫде разложенъ на шесть триѫгълника.

Нѣщата ставатъ още по-интересни при хептиамантитѣ, защото тамъ се появава връзка отъ по-високо ниво. Фигуркитѣ сѫ 24, всѣка състояща се отъ седемь триѫгълничета, което дава обща площь отъ 168 (колкото часоветѣ въ една седмица). Но 168 = 6 × 28 = 24 × 7, което означава, че трѣбва да се провѣрятъ форми съставени отъ 28 макро шестоѫгълника съ страна едно или отъ седемь макро шестоѫгълника съ страна двѣ. Рѣшения сѫществуватъ и въ двата случая: за седемь шестоѫгълника съ страна двѣ вж. фиг. 1, въ дѣсно, а за 28 шестоѫгълника съ страна едно фиг. 4.

Фиг. 4. Двадесеть и осемь шестоѫгълника съ страна едно могатъ да бѫдатъ покрити съ двадесеть и четиритѣ хептиаманти.

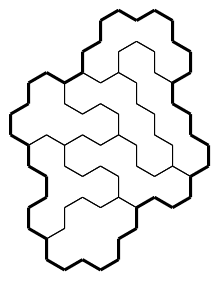
Красивото въ случая съ малкитѣ макро шестоѫгълници е, че броятъ имъ съотвѣтства на общата площь на тетрахексоветѣ. Формата отъ фиг. 4 може да се нареди съ тѣхна помощь по начина, показанъ на фиг. 5.

Фиг. 5. Това рѣшение отъ тетрахексове е единствено.

Колкото и елегантна да е тази връзка между хептиамантитѣ и тетрахексоветѣ, смѣтамъ, че тя е напълно случайна и нѣма нѣкакво по-дълбоко обяснение отъ чистия "капризъ на числата", който опрѣдѣля, напримѣръ, кое число да е просто и кое съставно. Провѣрка въ Онлайнъ енциклопедията на поредицитѣ отъ цѣли числа (фигурки отъ триѫгълници безъ дупки, фигурки отъ шестоѫгълници), показва, че единствената друга такава връзка е между единия дихексъ и тритѣ тетриаманта, които обаче не могатъ да се подредятъ въ формата на два слѣпени шестоѣгълника.

Макро структури сѫ възможни и при полихексоветѣ. 28-тѣ тетрахексове могатъ да се подредятъ въ четири голѣми шестоѫгълника, както е показано на фиг. 6.

Фиг. 6. Четиритѣ макро шестоѫгълника могат да бѫдатъ подредени само въ формата на посоченитѣ три тетрахекса, увеличени двойно. Първото рѣшение е уникално, за втората форма има десеть рѣшения, а за третата двѣ.

Въ малкитѣ комплекти хексове не сѫществуватъ други интересни макроструктури (отъ шестоѫгълници или триѫгълници).